Bu yazıda adil bir seçim üretme çabasını ortaya koyan Condorcet oylama yöntemlerine göz atalım. Sonunda da bizi yeni bir paradoks bizleri bekliyor.
On sekizinci yüzyıl Fransız asilzade Jean-Marie Marquis de Condorcet bir politikacı, anayasa avukatı, matematikçi ve yazardı. Hem siyasetçi hem de matematikçi olarak en ilgi çekici metinlerinden bazıları oylama ve seçim teorisi ile ilgiliydi.
Seçim paradoksu veya diğer seçenek paradoksu (ayrıca bilinen adıyla Condorcet’nin paradoksu), Marquis de Condorcet tarafından 18. yüzyılın sonlarında tespit edilmiş bir durumdur. Bireysel
tercihlerin döngüsel (geçişli olmayan) olmasa bile birikimli tercihlerin olabileceğini ifade eder.
1785 yılında Condorcet, “Essai sur l’application de l’analyse à la probabilité des décisions rendues à la pluralité des voix” (Olasılık analizinin çoğunluk kararlarına uygulanması üzerine deneme) başlıklı iki yüz sayfalık bir makale yazdı.
Condorcet, makalesinin altmış birinci sayfasında okuyucuya ünlü paradoksu sundu. Adı, bu nedenle tüm zamanlarının en büyük sosyal bulmacalarından biriyle ilişkilendirildi. Günümüzde seçim işlevleri ve ilgili soruların incelenmesi, oyun teorisinin bir alt alanı olan sosyal seçim teorisi olarak adlandırılır.
Matematikçiler Neden Seçimlerle İlgilenir?
etaylara geçmeden önce seçim sistemleri ve matematik arasındaki ilişkiyi anlamaya çalışalım. Demokraside yeni bir hükümet kurma zamanı geldiğinde seçim yapılır. Bunun içinde halk oy kullanmak için sandık başına gider.
Milyonlarca oy pusulası daha sonra bir sonraki seçilmiş yetkilinin kim olduğunu belirlemek için sayılır. Ancak her tür oylama sistemi, adaletini sorgulanabilir kılan sorunlarla karşılaşır. İşre tam da bu nedenle matematikçiler uzun süre adil bir seçim sistemi bulmak için de çabalamışlar ve sonucunda birbirinden farklı isimlerle karşımıza çıkan yöntemler bulmuşlardır.
Birazdan detaylarını paylaşacağımız Marquis de Condorcet ise çoğunluk tarafından karar verme kriterini benimsemenin doğasında var olan zorluğu bizlere göstermişti.
Marquis de Condorcet ( 1743-1794). Marquis de Condorcet bu paradoksu 1785’te tanımladı
Çok sayıda adayın olduğu ve çok sayıda seçmenin adaylar hakkında görüş bildirdiği seçimlerde Condorcet yöntemi bir anlamda mümkün olan en iyi oylama sistemidir. Condorcet yönteminde, her seçmenin seçimleri bir dizi turnuvada diğer herkesle karşılaştırılscaktır.
Condorcet Yöntemi İle Seçim Nasıl Yapılmaktadır?
Bir aday tüm turnuvaları kazanırsa, genel olarak kazanır. Eğer bu karşılaştırmaların sonucunda kazanan bir aday varsa da Condorcet kazananı olarak adlandırılır. Ancak ne yazık ki gerçek seçimlerde çok sayıda seçmen ve aday olduğu için bu sistemi uygulamak çok olası değildir.
Konuyu anlamak için A, B ve C olmak üzere üç aday ve 30 seçmen ile gerçekleştirilen bir seçimi ele alalım. Seçim sonucu aşağıdaki gibi olsun. ( A>B dendiği zaman bir seçmenin A’yı B’ye tercih ettiğini anlamanız gerekiyor)
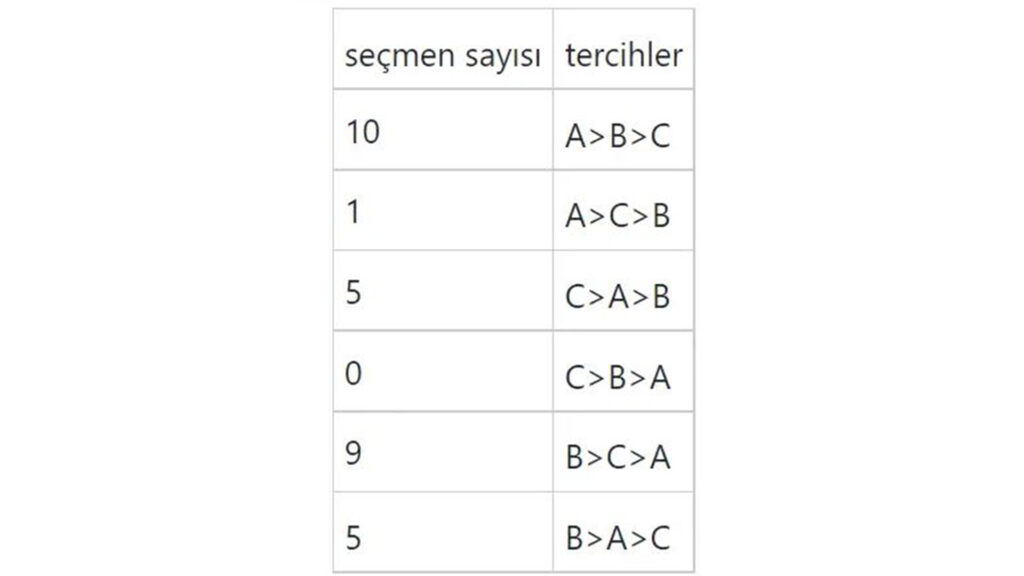
Bu seçimde A, B’yi 16 kez ve B’de A’yı 14′ kez yener. Yani A ile B yi karşılaştırdığımız zaman A iki oy öndedir. Şimdi A ile C’ye bakalım. Gördüğünüz gibi A, C’yi yine 16 kez yener. C ise , A’yı 14 kez yener, yani yine A, C’nin 2 önündedir. Şimdi de B ile C’ye bakmamız gerekiyor. B, C’yi 24 kez yener ve C’de, B’yi 6’kez yener. Bu nedenle B açık ara C’nin 18 oy önündedir. Şimdi tüm bunları bir şema ile gösterelim.
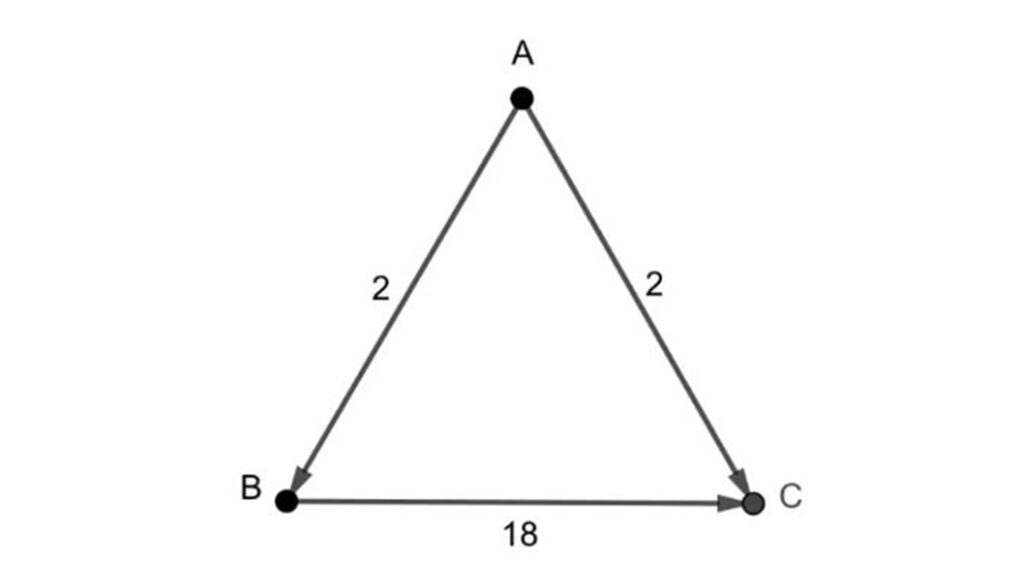
Sizin de gördüğünüz gibi bu yönteme göre seçimi kazananı yani Condorcet kazananı A olmalıdır. Ancak ne yazık ki işler her zaman bu örnekteki kadar kolay yürümez. Bu mantıkla bir kazanan bulmak kimi zaman mümkün olmaz. Bunun klasik bir örneği taş-makas-kağıt oyunudur.
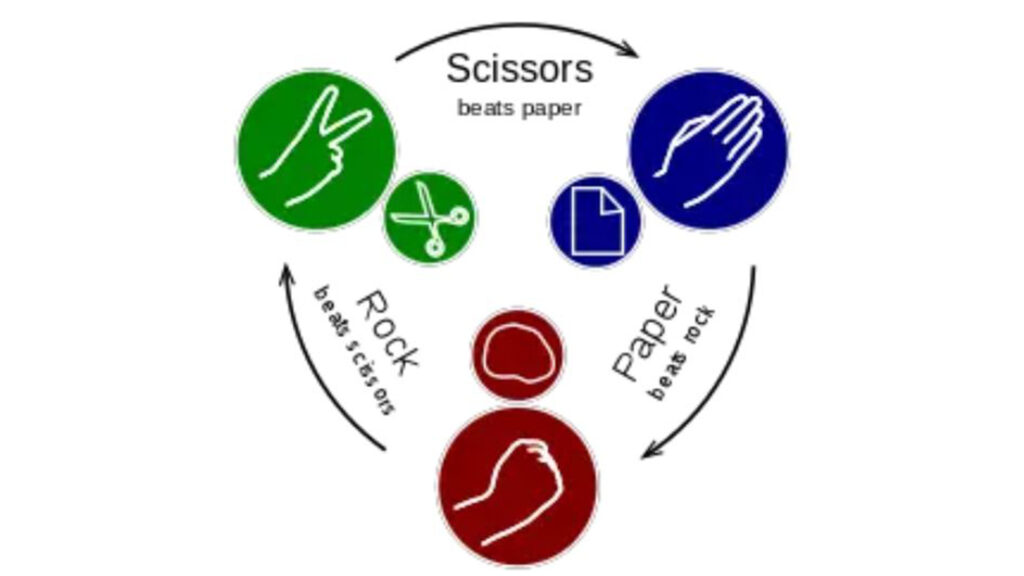Taş, makası kırar (Taş kazanır). Makas, kâğıdı keser (Makas kazanır). Kâğıt, taşı sarar (Kâğıt kazanır). Bu oyun genellikle bir iddia karşısında kazanını belirlemek için bir kaç kez oynanır. Bu
durumda da üç kez kazanan ilk kişi iddiayı da kazanmış olur.
Bu örnekte, taş makası yener, kağıt taşı yener ve makas kağıdı yener. Peki kim kazanır? Hiç kimse. Buna döngüsel durum denir ve Condorcet kazananı yoktur.
Condorcet Kazananı Bulmak Mümkün mü?
Şimdi biraz daha karmaşık bir seçime göz atalım. Bu seçimde 7 seçmenimiz ve dört tercih olsun. Seçim sonucunda sıralamaları aşağıda görebilirsiniz. Yanında da sonuçları bir şemada inceleyelim. Şemada örneğin B’den C’ye giden ok, B’nin C’yi 3 oy farkla mağlup ettiğini gösterir.
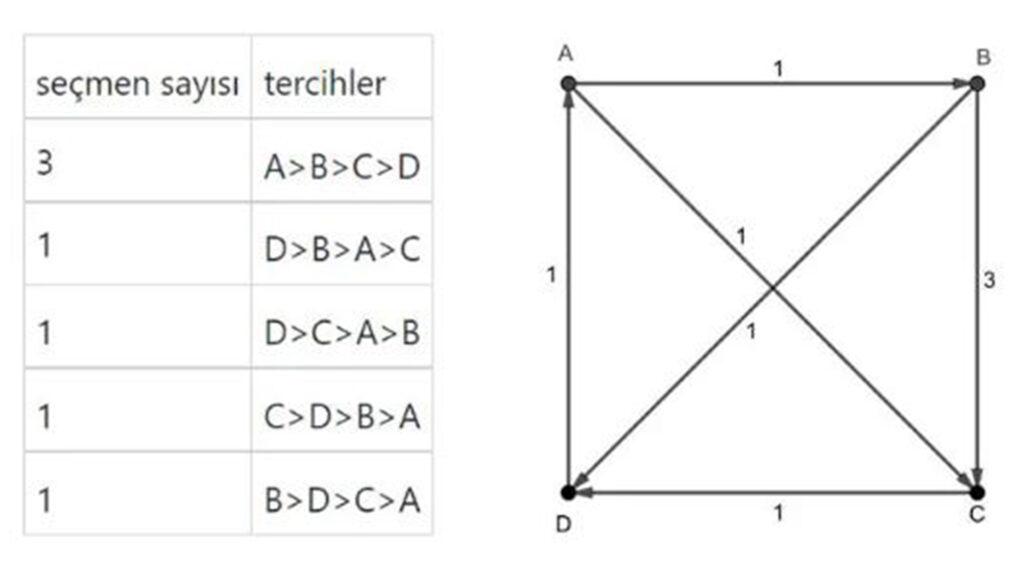
Yukarıdaki sonuçlara baktığınız zaman seçimi kazanan kişinin A olduğunu düşünmeniz olasıdır. Ancak ikili karşılaştırma yaptığınız zaman bu durum değişir. A, B’yi 4 kez ve B’de A’yı 3 kez yener. Yani A ile B yi karşılaştırdığımız zaman A bir oy öndedir.
A ile C içinde aynı sonuç geçerlidir. A ile D’yi karşılaştırdığınız zaman da D, A’yı 1 oy farkla geçecektir. B ile C’ye baktığımız zaman oy farkı 3 olur. B ile D arasında da bu fark 1’dir. ( Sayarak hesaplayabilirsiniz).
Dikkat ettiyseniz ikili karşılaştırmalarda hem A hem de B iki defa kazanıyor. C ve D’de birer kez kazandı. Bu durumda Condorcet kazananı yoktur. Üç veya daha fazla seçenek olduğunda, seçmenlerin tercihleri arasında çoğunluk oylaması bir döngü oluşturacaktır.
Günümüzde biz de bu duruma Condorcet paradoksu diğer adıyla seçim paradoksu diyoruz. ( Seçenekler arasındaki farkın yalnızca tek bir belirgin boyutu varsa (Sağ- sol parti gibi), o zaman Condorcet paradoksu oluşmayacaktır.)
Oylama Sistemleri İle İlgili Sorun Çözüldü mü? Döngüsel durumlarla başa çıkabilen ve bir kazanan sunan bir dizi başka oylama stratejileri de geliştirilmiştir. Matematikçi Jean-Charles de Borda (1733–1799) tarafından önerilen Borda yöntemi adayların seçmenlerin tercihlerine göre sıralanması gereken birçok durumda halen kullanılmaktadır.
Ancak ne yazık ki uygulama esnasında bu yöntemde de başka sorunlar çıkmaktadır. Sonuç olarak, tüm oylama sistemlerinin bir şekilde kusurlu olduğunu kabul etmeliyiz.
